(1.桂林航天工业学院 无人遥测重点实验室,广西 桂林541004;2.桂林电子科技大学 电子工程与自动化学院,广西 桂林541004)
为了解决低成本小型无人机航姿精密测量的问题,设计了一种基于MARG传感器的航向测量系统方案。该系统由MEMS IMU、电子罗盘和STM32F407微处理器组成,采用运算量较小的梯度下降算法和改进型二阶互补滤波算法将具有互补特性的电子罗盘和IMU进行数据组合滤波, 并基于四元数进行坐标转换,解算出飞行器航向信息。通过对航向测量系统的实验测试及其在旋翼飞行器上的验证分析,结果表明,在没有外界信息辅助的情况下,该系统较好地解决了噪声干扰与航向测量问题,可以满足小型旋翼无人机对航向信息的要求。
中图分类号:V249
文献标识码:A
DOI:10.16157/j.issn.0258-7998.173121
中文引用格式:王勇军,李智,李翔. 采用组合滤波算法的无人机航向测量系统研究[J].电子技术应用,2018,44(2):39-43.
英文引用格式:Wang Yongjun,Li Zhi,Li Xiang. Research of heading measurement system for UAV based on combined filter[J]. Application of Electronic Technique,2018,44(2):39-43.
?引言
航向是无人飞行器的重要飞行参数,在飞行过程中,实时准确地获得飞行器的航向信息决定了飞行器的可靠性和稳定性。如今随着微电子技术的发展,小型低成本旋翼无人飞行器普遍采用基于微机电系统(MEMS)的三轴陀螺仪、三轴加速度计和三轴磁强计来测量航向[1]。由于MEMS传感器自身存在非正交误差,以及数据积分产生的发散误差和外部干扰产生的随机误差,因此需要对多传感器进行误差处理并寻求最佳数据融合算法,才能得到精确的航向信息。
目前多数由陀螺仪和磁强计组成的航向测量系统主要采用罗差修正法和卡尔曼滤波算法来计算航向信息[2]。采用罗差修正的方法对磁强计进行校正,虽然能提高一定的精度,但仅针对磁传感器校正仍然无法提高系统在受到长时间低频干扰时的航向精度;而卡尔曼及其扩展算法可对磁强计和陀螺仪进行信息融合,能有效平滑曲线,使高频误差得到抑制,但无法消除磁强计受到的软硬磁干扰误差,而且应用时需要为其建立可靠稳定的状态方程,确定合适的量测噪声和过程噪声协方差矩阵,需要较大的时间开销。
为此,本文设计一种基于MEMS惯性测量单元(IMU)和电子罗盘的航向测量系统,采用梯度下降算法来对磁强计和陀螺仪进行误差修正,而且在姿态解算过程只需进行乘法和加法运算,普通的微控制器即能满足算法要求[3]。另外,在MAHONY R提出的补偿滤波器[4]的基础上进行优化改进,结合二阶互补滤波算法来进行数据融合,以期得到精密航向输出。
1 无人机航向角描述与系统方案设计
1.1 坐标系定义及姿态矩阵
无人机的航姿信息主要包括航向角(也称航偏角)、俯仰角θ、横滚角γ。选取“东北天”为地理坐标系(记为ENU系),“右前上”为机体坐标系(记为NED系),由于NED系和ENU系均是直角坐标系,且各个轴之间始终保持垂直,因此,NED系和ENU系的空间位置关系即可理解为刚体的定点转动[5]。地理坐标系与机体坐标系之间的角度转换关系如图1所示。
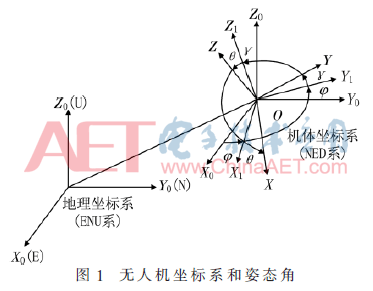

1.2 系统方案设计
该航向测量系统硬件主要由MEMS-IMU、MEMS电子罗盘和主控制器组成,如图2所示。其中MEMS-IMU采用的是InvenSense公司的MPU-6500,它由一个三轴陀螺仪和三轴加速度计组成,可以通过SPI口输出飞行器的角速度、加速度等姿态信息,用来计算俯仰角及横滚角;所采用的MEMS电子罗盘是ST(意法半导体)公司的LSM303D,它内部的三轴磁强计可通过SPI总线口输出测得的磁场数据,另外,它内部的三轴加速度可用来测量重力矢量,获得载体的倾角信息,并通过运算补偿航向信息的输出。主控器采用ST公司CM4内核的32位ARM微控制器STM32F407,主要通过获取MEMS传感器的输出数据进行姿态解算,完成飞行器航向的精密测量。

由于IMU中的陀螺仪、加速度计和电子罗盘中的加速度传感器都可以测量加速度信息,因此该系统的传感器配置也是具有一定冗余度,主控制器的另一任务就是将各传感器的数据取长补短进行数据融合,提高姿态解算精度。主控制器读取出传感器采集到的原始数据,利用梯度下降法优化电子罗盘中加速度计和磁强计的输出数据,获得静态性较好的姿态四元数,然后利用改进型互补滤波器将其与IMU获得的动态性较好的姿态信息进行融合滤波,最后通过四元数的坐标换算解算出航向角。
2 航向数据组合滤波算法设计
2.1 梯度下降法
梯度下降算法是一种迭代求极值的算法,具体实现过程是按目标函数斜率的负方向来搜索寻优。电子罗盘中的加速度计和磁强计具有良好的静态特性,长时间使用不会引入积分误差,但是加速度计受载体振动和运动影响较大,动态环境下,瞬时误差大,而且磁强计容易受到周边环境中软硬磁干扰[7],因此本文首先使用梯度下降算法加对速度计和磁强计输出数据进行优化,获得一个静态特性较好的姿态四元数,然后再进行下一步航向解算。

显然f(q)≥0,进而对姿态四元数的优化就可以转换为对f(q)求最小值。
梯度下降法在姿态解算过程中只有简单的加法和乘法运算,此时四元数更新方程可变为[8]:

2.2 改进型互补滤波算法
利用电子罗盘中三轴磁强计和加速度计测得的数据通过梯度下降法对姿态四元数进行修正转换后得到姿态值记为。根据加速度计和磁强计的特性,不会引入累积误差,但是在动态情况下,会引入较大瞬时误差。相反IMU中的陀螺仪可测得瞬时精度高的姿态数据,但是有累积误差。设IMU中陀螺仪和加速度计直接积分解算出来的姿态值为,根据和在频域上的互补特性,通过传统的互补滤波方法融合两者,可得到新的姿态值,虽然能同时消除低频和高频的干扰,实现姿态数据的融合,然而,互补滤波器[9]的低通阻带衰减缓慢,误差较大时,振动大,滤波效果差。因此在传统互补滤波器的基础上添加了PI(比例积分)环节,构成改进型二阶互补滤波器,如图3所示。
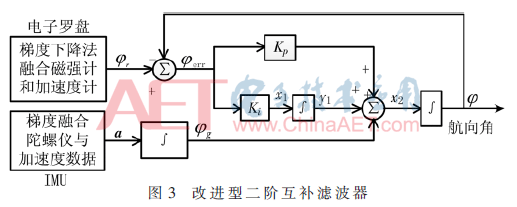
由图3可知:

2.3 航向角组合解算
系统基于四元数的姿态计算即对式(1)中的姿态四元数的微分方程进行求解,四元数微分方程常用的解算方法有[10]:单子样旋转适量法、多子样旋转矢量法、龙格库塔法和泰勒展开法。旋转矢量法多用于输出是角增量的陀螺仪, 而MEMS陀螺仪的输出形式是角速率。考虑到运算精度和速度, 本系统采用四阶-龙格库塔法求解微分方程:
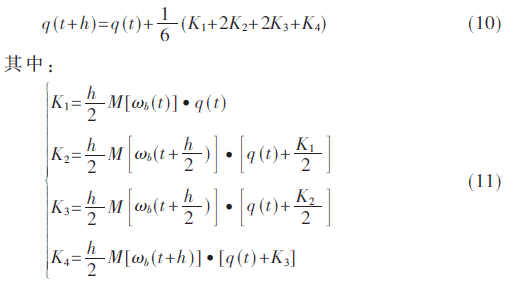
式中,h为姿态数据采样的周期,即四元数更新周期;ωb(t)、、ωb(t+h)分别为在更新周期h时间内陀螺的采样值。每个采样周期内提取陀螺仪的数据,对式(10)进行迭代运算,便能够实现对四元数的实时更新,从而得出航向角。
3 实验验证分析
将设计的航向测量系统安装在电子转台上,为避免铁磁干扰,加工一个60 cm高的木架做固定支撑,并校正好零位,通过串口连接至上位机,进行传感器数据采集,如图4所示。

通过电子转台水平转动,每次回到零位时利用上位机分别采集电子磁罗盘的数据和经过梯度下降与互补滤波算法融合后的数据。通过对比分析可知,没有使用滤波算法的磁强计测量的航偏角相对零位误差较大,达到了±3°左右,磁强计受外界干扰严重。经过组合滤波处理后得到的偏航角消除了部分干扰信号,误差可稳定保持在±1.0°以内。
在电子转台上转动测试可看作是静态测试,为进一步验证航向测量系统在多旋翼飞行器实际飞行过程中的性能,将该系统固定在PIX4飞控模块屏蔽罩上,并一同安装在六旋翼飞行器上,机架底部水平固定在万向节一端,万向节另外一端固定在水平的桌面上,如图5所示。

启动旋翼飞行器电机,将飞行器油门通道值保持在空中悬停状态,操作飞行器方向舵,让其原地旋转。然后,通过2.4G串口数传电台接收飞控航向数据和航向测量系统传出的磁强计、陀螺仪原始数据以及组合解算后的数据,并用MATLAB进行数据分析,如图6所示。
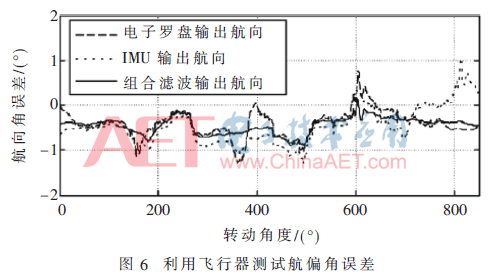
图6中采集的是飞行器水平悬停转动(以飞控为基准)时的数据,其中的电子罗盘和IMU输出航向分别代表的是磁强计和陀螺仪数据处理的航向角误差曲线,组合滤波输出航向表示经梯度下降和二阶互补滤波算法融合后解算的航向角误差曲线。旋翼飞行器运动过程中受电机工作引起的机架振动、载体重力分布不均、机械连接处阻尼问题等因素影响,导致航向角误差比水平放置在转台上时的静态零点误差偏差相对较大且波动相对厉害,经过组合滤波处理后,航向角误差在±1.5°以内,可以满足小型旋翼飞行器对航向数据的要求。
4 结论
航向信息作为无人飞行器导航定位的重要测量参数,要求具有较高的精度。在小型旋翼无人飞行器系统上,利用MEMS IMU和电子磁罗盘各自的优点及其互补性,配合ARM主控制器组成低成本航向测量系统,采用梯度下降和二阶互补滤波算法,使三轴陀螺仪、三轴加速度计、三轴磁强计经过数据融合后,完成坐标变换和姿态解算,从而输出较高精度的航向角。实验结果表明:该航向测量系统较好地解决了噪声干扰与航向最优估计问题,并在实验平台上得到了验证,航偏角误差保持在±1.5°以内,在没有外界信息辅助的情况下,可稳定地输出准确姿态数据,满足了低成本旋翼无人机对航向信息的要求。
参考文献
[1] 何川,李翔,王勇军.基于STM32的四旋翼飞行器的姿态最优估计研究[J].电子技术应用,2015,41(12):61-64.
[2] 任爱爱,孙永荣,胡应东,等.无人机航向测量抗差补偿滤波技术研究[J].传感器与微系统,2009,28(5):34-36.
[3] MADGWICK S O H,HARRISON A J L,VAIDYANATHAN R,et al.Estimation of IMU and MARG orientation using a gradient descent algorithm[C].IEEE International Conference on Rehabilitation Robotics,2011:1-7.
[4] MAHONY R,HAMEL T,PFLIMLIN J M.Nonlinear complementary filters on the special orthogonal group[C].IEEE Transactions on Automatic Control,2008,53(5):1203-1218.
[5] 秦永元.惯性导航[M].北京:科学出版社,2014.
[6] 曾宪阳,杨红莉,郁汉琪.基于STM32单片机四旋翼飞行器建模分析与设计[J].电子技术应用,2016,12(42):65-68.
[7] 聂鹏,李佩华,李正强,等.基于卡尔曼滤波的小型无人机姿态估计算法研究[J].沈阳航空航天大学学报,2013,30(6):53-57.
[8] 谭广超.四旋翼飞行器姿态控制系统的设计与实现[D].大连:大连理工大学,2013.
[9] 廖懿华,张铁民,廖贻泳.基于模糊-比例积分偏差修正的多旋翼飞行器姿态测算系统[J].农业工程学报,2014,30(20):19-27.
[10] 王彤,马建仓,秦涛,等.基于旋转四元数的姿态解算算法[J].弹箭与制导学报,2014,34(3):15-17.





















